【图形学 I】线性代数

前排提醒

我数学很差，如果哪里整错了求纠正！

图形学相关线性代数

本文转门学习一些和图形学相关的线性代数基础知识，不深究。

向量

表示

不多说。

向量长度

如果是个二维向量，设。

提醒

这里的向量坐标都用纵向的矩阵，为啥呢？老师是这样教的。横向的也一样用。下面的转置和这个相关。

勾股定理：

矩阵相乘：

单位向量的长度是。

向量对应矩阵转置

具体请看矩阵部分的转置。

如果是个二维向量，设。

那么它对应的矩阵

转置：

点积

如果和是两个二维向量，设，。三维的就设个哪来那么多问题！！

高中数学。

单位向量：

点积满足交换律、结合律、分配律。

点积的几何意义：

若，则两向量夹角在到。

若，则两向量夹角是。

若，则两向量夹角在到。

还有投影。

叉积

XG!

左手系和右手系的区别：

红色x轴，蓝色z轴，绿色y轴。

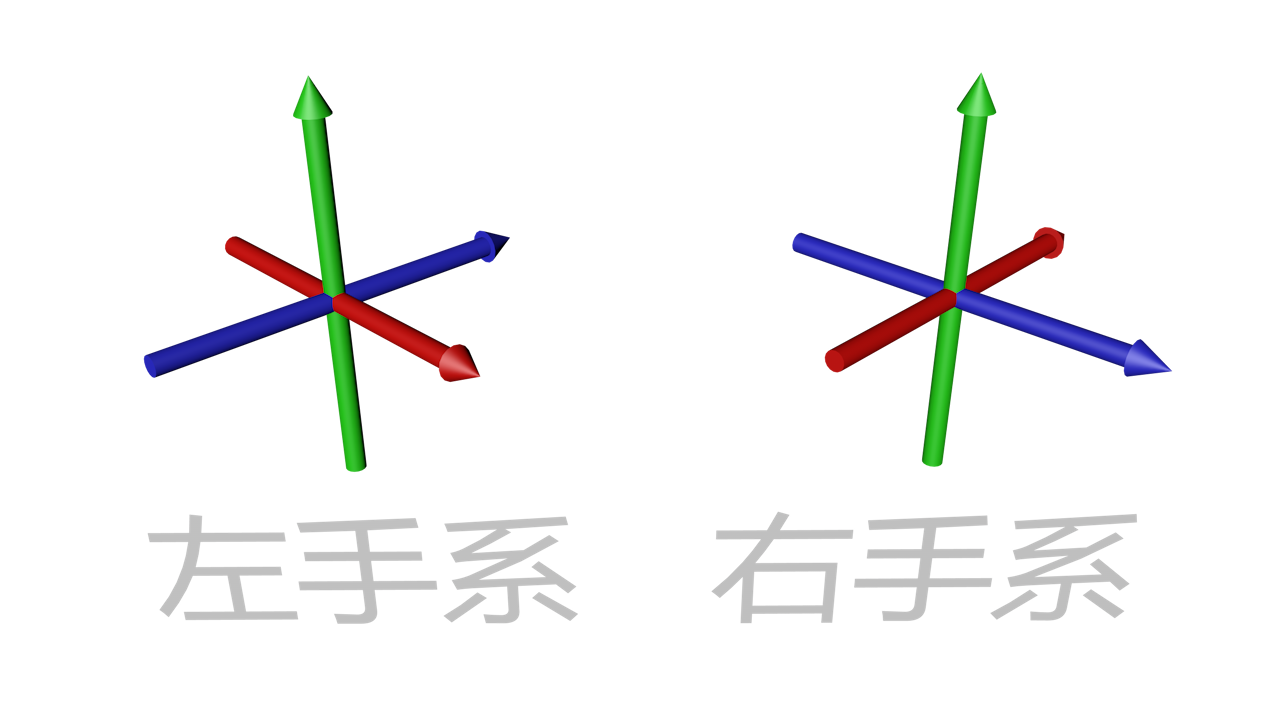
提醒

之后的东西统一都用右手系。

叉积可以算和两个向量垂直的那个向量。

比如右手系中的这几个轴：

明显可见叉积不满足交换律。

如果用的右手系，那么可以使用右手螺旋定则。

四指为叉积中前者到后者的方向，拇指为结果的方向。

二维

如果和是两个二维向量，设，。

呜呜呜行列式忘了怎么算了。

三维

如果和是两个三维向量，设，。

矩阵

表示

转置

乘法

乘法的结果会继承前者的行数与后者的列数，而且前者的列数必须等于后者的行数。

也就是说上面那两个矩阵可以相乘，最后得出的矩阵是个的。

结果第i行j列的数是前者i行与后者j列的点积。太难算了不算了！

单位矩阵

都是方阵。

逆矩阵

，那么

是伴随矩阵，是对应行列式。

先求伴随矩阵。

设

代数余子式：

好难写通式……

举例子吧

那么

好了，套这个就好了！